ABSTRACT

The existence of a vector field is shown. This field is originated by all moving inertial masses, and it exerts a force on all other nearby moving masses.

This field has a relation with the gravitational field which is analogous to that between the electrical and magnetic fields, therefore I propose the name "Gravnetic" for this field.

The existence of the Gravnetic Field is implied by the Special Theory of Relativity as shown here.

Based on a varying gravnetic field, generated by a mass flow of variable velocity, one can produce gravitational-gravnetic waves.

STATEMENT

For any observer for which there is a mass flow, also does exist a vectorial field V which surrounds that mass flow.

The vectorial field V exerts, on any one mass which moves with speed U' non-parallel to V, a force F, in a direction normal to the plane defined by U' and V.

The intensity of this field V depends on the flow density and speed, and it is inversely proportional to the distance from the flow.

DEMONSTRATION

Let it be the scene, depicted in the following figure, composed of the following elements:

• An observer A, at rest relatively to an inertial reference frame
• A mass flow which has speed U relative to the A observer
• An observer B, moving relative to A with speed U in the same direction as the flow measured by A
• An object W, at a distance r from the flow axis, with mass m' and speed U' in direction parallel to U, both as measured by A

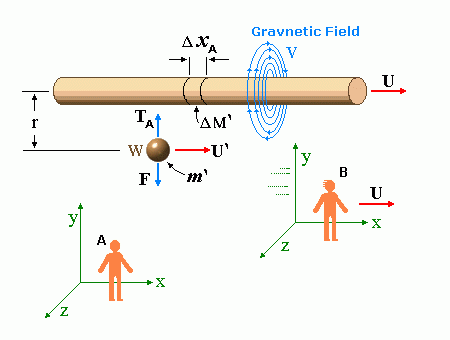Let c be the speed of light in free space. Applying the Special Theory of Relativity to get the speed U'' of the W object, relative to the B observer, we have: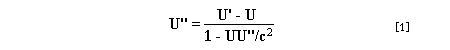

As far as the speed of light imposes a limit, we can make three variable substitutions, measuring all three velocities as fractions of that of light: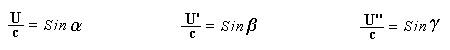

According to these definitions of the new Alfa, Beta and Gamma variables, it holds that:

Applying these relations to the [1] equation, we get: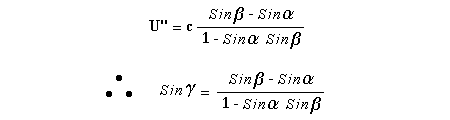

And, as:

Therefore, we can make the following successive transformations: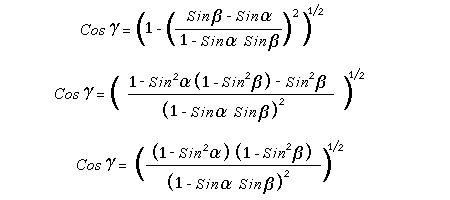

And also, as:

then we get: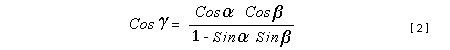

Now, let us consider a differential mass element from the flow. This element has a length delta of X_A and a mass delta of M', as measured by the A observer, so this observer defines the linear density of the flow as: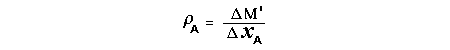

But, being delta of M the mass at rest (i.e. relative to B) of the flow element, we know that the relation between the mass delta of M' measured by A and the mass at rest is: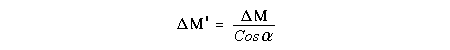

and then: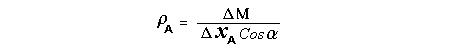

Also, by the Lorentz length-contraction, the length delta of X_A, measured by the A observer, has the following relation with the length at rest delta of X_B (as measured by B):

Therefore, the linear density measured by A, written using the mass and length at rest, is: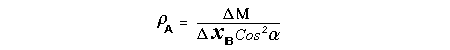

Now, as the linear density measured by B, who rests relative to the flow element, is: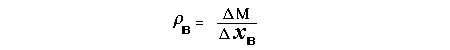

Then, the relation between the linear densities measured by A and by B is: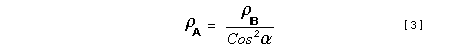

Turn we our attention now to the gravitational field created by the mass which A perceives as a flow.

Let suppose that the length of this (flowing) mass in the direction of U is much greater than r, then the gravitational intensity N_B at the distance r measured by B, which rests relative to this beam, is that corresponding to a long mass with negligible thickness: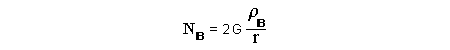

where G is the Gravitational Constant.

The W object, which has a mass at rest m, relative to the B observer it has a mass:

as W moves in relation to B with speed U''.

According to this, the force T_B exerted on m'' by the linear distribution of mass, is measured by B as:

which is the same as:

Now, from the inertial reference-frame of A the gravity intensity N_A, at the distance r from the flow axis is:

and substituting according to [3] it becomes:

and, as relative to A the mass of W is m', then, the gravitational force on W as measured by A is: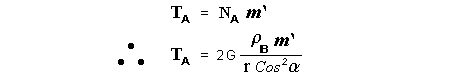

but, as the mass m', relative to the mass at rest, is:

then: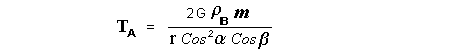

which, according to [4] can be transformed into:

and, by [2], it is the same as:

Also, according to the mathematical relation:

so, we have the following relation between the forces on W as measured by A and by B:

On the other hand, from the expression [6] we also get the relation:

Now, according to the Special Relativity: If P is the total transverse force on an object W, with mass at rest m, then the total transverse forces P_A and P_B measured by observers A and B which are moving in relation to W, follow the transformations:

which give: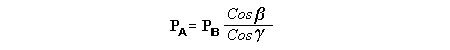

and, by substituting the denominator according to [2] we get: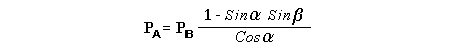

For the B observer, the total force between the linear mass and W is only the gravitational one, so:

wich implies that: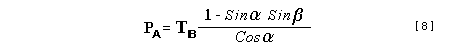

By comparing [8] with [6] we see that P_A is different from T_A, in the general case.

which, according to [8] can be transformed into: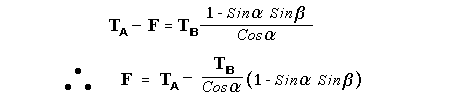

and by using [7] we get: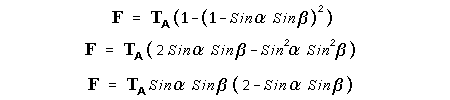

We can replace the force T_A as the product of the field N_A and the mass m', so:

which according to [5] is the same as:

If we now define the flow intensity as mass per unit time:

Then, the linear density as measured by A, considering an differential element, can be transformed as follows: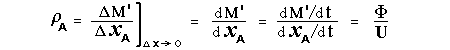

and then:

which, returning to variables of speed, becomes:

And, if we define the "Gravnetic Constant" G_N as:

then the "Gravnetic Force" may be expressed as:

This document in PDF:  



Link: The VIRGO Project to detect gravitogravnetic waves








Copyright © 1988-2008 Luis Guillermo RESTREPO RIVAS, All Rights Reserved